[Enter Post Title Here]
SVEUČILIŠTE U ZAGREBU
FAKULTET ELEKTROTEHNIKE I
RAČUNARSTVA
ZAVRŠNI RAD br. 1731
Uporaba genetskih algoritama za
rješavanje problema krojenja
Ante Modrić
Mentor: Doc.dr.sc.
Marin Golub
Zagreb, Lipanj, 2011.
Sadržaj
3. Genetski algoritmi prilagođeni za problem krojenja
3.1. Algoritmi za rješavanje
1D problema krojenja
3.2. Algoritmi za rješavanje 2D problema krojenja
1. Uvod
U zadnjih
nekoliko desetljeća genetski algoritmi se, zbog svog izuzetnog omjera
brzine i kvalitete rješenja, koriste za rješavanje velikog broja problema
kombinatoričke optimizacije kao što su problem trgovačkog putnika,
problem spremanja kutija u kontejnere, raspoređivanje poslova po radnim
stanicama i slično. To su problemi kod kojih je pri većim problemima
teško ili nemoguće deterministički odrediti optimalno rješenje u
nekom razumnom vremenu (za dovoljno velike probleme može trajati danima). Jedan
od takvih problema je i problem krojenja materijala.
Problem krojenja
materijala se pojavljuje u mnogim industrijama: tekstilna, drvna, metalna,
novinska itd. Problem se pojavljuje u vidu gubitaka koji nastaju ako se
materijal ne izreže adekvatno, pa veliki dio propadne. U ovom radu definiraju
se problemi krojenja te se prezentiraju genetski algoritmi za rješavanje 1D i
2D problema krojenja. U 2. poglavlju je objašnjen problem krojenja, te navedene
neke klasifikacije različitih problema ovog tipa. Algoritmi za rješavanje
problema krojenja opisani su u 3. poglavlju. U 4. poglavlju navedeni su
implementirani algoritmi i problemi, provedena su ispitivanja
učinkovitosti implementiranih algoritama te usporedba kako razlike
među njima utječu na dobivene rezultate.
2. Problem
Problem krojenja
(eng. Cutting Stock Problem, CSP) je
problem kombinatoričke optimizacije koji uključuje rezanje
raspoloživog materijala u potrebne manje komade (predmete) sa ciljem da se
minimalizira broj korištenih komada raspoloživog materijala i količina
otpada.

Skupa sa problemom pakiranja
predmeta (eng. Bin Packing Problem,
BPP) pripada grupi problema pakiranja i rezanja (eng. Cutting and Packing, C&P) [1], među koje pripada i problem
utovara vozila, utovara paleta, problem pakiranja naprtnjače i mnogi drugi
slični problemi. Svi problemi iz te grupe problema se, ako im se
ograničenja podudaraju, mogu rješavati istim algoritmima. To je i razlog
što se za problem krojenja koriste isti algoritmi za koje se u literaturi
navodi da služe za rješavanje problema pakiranja predmeta.
Za rješavanje
problema krojenja (a time i ostalih C&P problema) se općenito koriste
2 pristupa: fokusiranje na objekte i fokusiranje na uzorke. Prvi pristup
direktno pridružuje zahtjeve za rezanjem komadima raspoloživog materijala, dok
drugi pristup prvo generira uzorke rezanja raspoloživog komada, a zatim
kombinira dobivene uzorke da bi se ostvarili svi zahtjevi za rezanjem. Prvi
pristup je prikladniji za korištenje ako postoji više veličina materijala,
dok su za jednu veličinu materijala oba pristupa jednako prikladna.
Problem rezanja
se formalno definira na sljedeći način: Zadana je lista od m predmeta koje je potrebno izrezati u qj komada (j=1, ..., m). Ako se svakom planu rezanja pridruži broj xi koji označava koliko će se puta i-ti plan rezanja iskoristiti, onda se
problem rezanja definira kao:
|
|
(2.1)
|
|
|
(2.2)
|
|
|
|
gdje je aij broj pojavljivanja
predmeta j u planu rezanja i, a ci
je cijena (najčešće ostatak) plana rezanja i [2].
Prema Dychoffovoj
tipologiji [1] problemi krojenja se razlikuju prema 4 glavne karakteristike:
1. Dimenzionalnost:
(1)
Jednodimenzionalni
(2)
Dvodimenzionalni
(3)
Trodimenzionalni
(N)
N-dimenzionalni sa N>3 (dimenzija problema, ne objekata)
2. Način dodjeljivanja
(B) Svi
materijali a odabir predmeta
(V) Odabir
materijala a svi predmeti
3. Izbor materijala
(O) Jedan
materijal
( I ) Više
jednakih materijala
(D) Više
različitih materijala
4. Izbor predmeta
(F) Mali broj
predmeta (različitih oblika ili dimenzija)
(M) Puno
predmeta u puno različitih oblika ili dimenzija
(R) Puno
predmeta u relativno malo različitih oblika ili dimenzija
(C) Jednaki
predmeti
Osim ove podjele,
dvodimenzionalni i trodimenzionalni problemi se dodatno razlikuju po još dva
ograničenja [3]:
• orijentiranost
– predmeti mogu biti fiksno orijentirani (O) ili se mogu rotirati za 90°
stupnjeva (R)
• giljotinski
rezovi - jedini dopušteni rezovi su giljotinski (rez koji cijepa materijal
ortogonalno po cijeloj dimenziji)(G) ili su dopušteni slobodni rezovi (F)
Treba još
spomenuti problem specifičan za 2D problem krojenja: problem krojenja
role. To je dvodimenzionalni problem krojenja kod kojeg se zna samo širina
materijala, dok se ukupna visina rezanih predmeta treba minimizirati.

3. Genetski algoritmi prilagođeni za
problem krojenja

Genetski
algoritmi (eng. Genetic Algorithm,
GA) spadaju u grupu algoritama koje nazivamo evolucijski algoritmi. To su
metaheuristički algoritmi koji rješenja problema nalaze imitirajući
prirodnu evoluciju. Na početku izvođenja genetskih algoritama,
generira se početna populacija rješenja, te se ta rješenja ocjenjuju
pomoću funkcije dobrote. Krenuvši od početne populacije ponavlja se
evolucijski proces, koji se sastoji od jednog kruga izvedbe genetskih operatora
(selekcija, križanje i mutacija), dok se ne pojavi dovoljno dobro rješenje (u
većini literature se koristi izraz "dovoljno dobro rješenje" jer
se može dogoditi da genetski algoritam ne može naći optimalno rješenje).
Prema tipu
selekcije i stvaranja novih jedinki genetske algoritme dijelimo na dva tipa:
eliminacijski (eng. steady-state)
genetski algoritam i generacijski genetski algoritam. Korak (tj. iteracija)
eliminacijskog algoritma se sastoji od odabira dva roditelja, iz kojih
upotrebom križanja i mutacije nastaje dijete. To dijete se zatim ubacuje u
populaciju tako da zamjeni neku od jedinki. Roditelji se u eliminacijskom
genetskom algoritmu često odabiru 3-turnirskom selekcijom, koja se sastoji
od toga da se iz populacije nasumično odabere 3 jedinke, od kojih se dvije
bolje uzmu za roditelje, a najlošija se zamjeni novom jedinkom. Kod
generacijskog genetskog algoritma se u jednoj iteraciji stvara jednak broj
novih jedinki kao što ih je bilo prije, tj. stvara se cijela nova generacija
rješenja. Roditelji za provođenje reprodukcije kod generacijskog genetskog
algoritma se, osim k-turnirskom selekcijom koja je već opisana, mogu
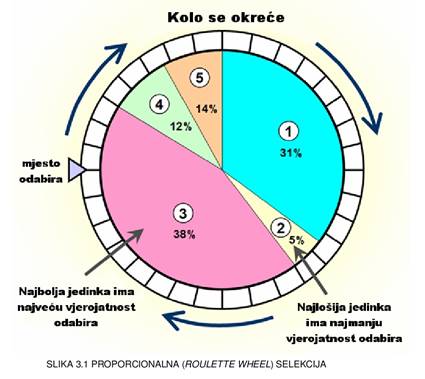
odabirati i proporcionalnom selekcijom (engl. Roulette-wheel selection, slika 3.1.). Kod proporcionalne
reprodukcije vjerojatnost svake jedinke da bude odabrana za stvaranje nove
jedinke je proporcionalna njezinoj relativnoj dobroti (kod velikih vrijednosti
dobrote, razlike u vjerojatnosti odabira najbolje i najgore jedinke bi prilikom
korištenja apsolutne dobrote postale zanemarive). Za razliku od eliminacijskog
genetskog algoritma gdje najbolja jedinka ne može nestati iz populacije, kod
generacijskog genetskog algoritma se to može dogoditi. Da bi se to
spriječilo koristi se elitizam, kojim se određen broj najboljih jedinki
(često samo najbolja) odmah dodaje u novu populaciju.
Bez obzira na to koju selekciju
koriste, oba tipa genetskih algoritama koriste jednake genetske operatore
križanja i mutacije, a oni ovise o načinu zapisa rješenja (genotip).
Postoje različiti načini zapisivanja rješenja, a oni ovise o problemu
koji se rješava. S obzirom na to da se genetskim algoritmima rješavaju problemi
optimizacije funkcija sa konačnim diskretnim domenama, najčešći
način zapisivanja rješenja je niz brojeva (iako postoje i drugačiji
zapisi, od kojih će jedan biti opisan u nastavku).
Genetskim
operatorom križanja od dvije jedinke roditelja nastaje nova jedinka dijete, a
mutacije se nasumice mijenjaju dijelovi rješenja koje predstavlja dijete.
Križanje služi kako bi se dobri dijelovi rješenja rasprostranili po cijeloj
populaciji, a mutacija kako bi se osigurala raznolikost rješenja u populaciji
te proširilo područje mogućih rješenja koje pretražujemo [4]. S
obzirom da su ovi operatori vezani za genotip koji se koristi, detaljni opis korištenih
operatora (i genotipa) nalazi se u nastavku teksta u opisu korištenih
algoritama.
3.1. Algoritmi za rješavanje 1D problema
krojenja
S obzirom na
raniji opis problema, lako se može zaključiti da problem krojenja pripada
grupirajućim problemima [5]. To su problemi kod kojih je cilj, na nekakav
optimalan način, smjestiti (grupirati) članove nekog skupa, u ovom
slučaju predmete, u odvojene podskupove tj. naći dobru podjelu skupa.
U skladu s time kod grupirajućih problema funkcija dobrote, koju treba
optimizirati, definirana je nad skupom svih valjanih grupacija (s obzirom na
posebne uvijete problema, najčešće postoje grupacije koje su
zabranjene). Za rješavanje takvih problema koristi se grupirajući genetski
algoritam (eng. Grouping GA, GGA).
3.1.1.
Grupirajući genetski algoritam
Grupirajući
genetski algoritam, kao što mu ime kaže, koristi grupe kao građevnu
jedinicu genotipa. Dok većina ostalih genetskih algoritama za prikaz
rješenja koristi polje brojeva, grupirajući genetski algoritam koristi
polje grupa, tj. svaki gen predstavlja grupu predmeta a ne jedan predmet. Grupe
se sastoje od popisa predmeta koji se trebaju rezati te duljina materijala od
kojeg se režu (Slika 3.2.). Prednost ovakvog zapisa je u tome što je broj gena
u rješenju varijabilan a poredak gena u rješenju nema nikakvo značenje,
kao ni poredak predmeta u grupi. Ako se usporedi ovakav zapis sa zahtjevima
problema koji se rješava, može se vidjeti da je potpuno prikladan.

Za rješavanje 1D problema krojenja
kod kojeg postoji više duljina materijala za rezanje, koristili su se operatori
vrlo slični onima koje su koristili Hinterding & Khan [6] (za probleme
gdje postoji samo jedna duljina materijala za rezanje pogledati [7]).
Jedinke
početne populacije se generiraju na način da se prvo slučajnim
odabirom odredi duljina materijala od kojeg će se grupa rezati, a zatim se
slučajno odabire predmet (od onih koji stanu i koji su ostali) koji
će se dodati u grupu za rezanje. Kad se tako grupa popuni, doda se u rješenje
i postupak ponovi dok se ne iskoriste svi predmeti koje treba rezati.
Korišteni
operator križanja radi na sljedeći način: grupe u svakom roditelju se
sortiraju uzlazno prema ostatku koji ostaje nakon rezanja (tj. uzlazno po
iskorištenosti). Dijete se gradi tako da se prvo 40% grupa iz prvog roditelja
prepiše u dijete, a zatim se redom prepišu sve grupe koji se mogu prepisati s
obzirom na ograničenja problema (broj predmeta koji se reže, količina
materijala itd.). Grupe koje se ne mogu prepisati se jednostavno preskoče.
Predmeti koji nakon ovakvog prepisivanja ostanu neiskorišteni se grupiraju na
isti način kao i kod generiranja početne populacije. Ovakvim
križanjem je osigurano da čak i ako se više puta odaberu isti roditelji,
dijete koje će rezultirati neće svaki put biti isto.
Operator mutacije
radi na način da se slučajno odaberu grupe koje će se brisati
(ostale grupe se prepišu u dijete), a od predmeta koji ostanu nakon brisanja
grupa se stvaraju nove grupe istim postupkom kao i kod generiranja populacije.
U raznim izvorima ([6],[7]) se za brisanje biraju samo lošije grupe da bi se
bolje grupe sačuvale, no s obzirom na to da je uloga operatora mutacije
raznovrsnost populacije te da odabrani operator križanja već daje
određenu prednost boljim grupama, mutacija ne diskriminira grupe prilikom
odabira za brisanje.
Osim što se
izvedba ovih operatora razlikuje od izvedbe operatora u
"običnim" genetskim algoritmima, razlikuje se i njihova
upotreba. Dok kod ostalih genetskih algoritama nove jedinke nastaju (s nekom
vjerojatnošću) križanjem te se zatim mutiraju, kod grupirajućeg
genetskog algoritma nove jedinke, zbog sličnosti između zadnjeg
koraka križanja i mutacije, mogu nastati ili samo križanjem ili samo mutacijom.
Za računanje
dobrote koristi se formula ![]() gdje
je C funkcija cijene [6] koja glasi:
gdje
je C funkcija cijene [6] koja glasi:
|
|
(3.1) |
gdje je:
wi = otpad nakon rezanja i-tog komada materijala
li = duljina i-tog komada materijala
ws = ukupan broj neiskorištenih komada
materijala (komadi materijala kojima je ostatak veći od maksimalnog
dopuštenog)
n = ukupan broj korištenih komada materijala
Svaki genetski
algoritam ima određene parametre. Kod grupirajućeg genetskog
algoritma tu spadaju: veličina populacije, broj generacija, vjerojatnost
križanja, vjerojatnost mutacije te elitizam. Prema [8] (Slika 3.3.) parametri
se mogu postavljati prije pokretanja programa (podešavanje parametara) ili
tijekom pokretanja programa (kontrola parametara).
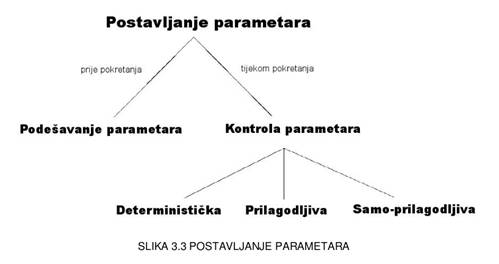
Podešavanje parametara prije
pokretanja se zbog složenog međusobnog utjecaja parametara
najčešće radi eksperimentalno. Kontrola parametara tijekom pokretanja
programa se može raditi deterministički, adaptivno ili samo-adaptivno.
Deterministička kontrola parametara znači da se parametri tijekom pokretanja
mijenjaju po nekom unaprijed određenom pravilu, bez ikakve povratne
informacije od algoritma, dok adaptivna kontrola parametara znači da
promjene parametara ovise o stanju u kojem se algoritam nalazi (devijacija
populacije, blizina lokalnog ili globalnog minimuma i sl.). Kod samo-adaptivne
kontrole parametara, parametri su zapisani u genotipu populacije, te skupa s
njim prolaze kroz križanje odnosno mutaciju.



3.1.2. Hibridni
grupirajući genetski algoritam
Kako bi se
poboljšao rad genetskih algoritama (ali i drugih heurističkih metoda)
često se uz njih koriste i drugi algoritmi za determinističko
rješavanje istog problema. Takvi se algoritmi onda zovu hibridni genetski
algoritmi (eng. Hybrid Genetic Algorithm,
HGA).
Pošto većina
genetskih algoritama služi da bi se neka funkcija optimizirala, uz njih se u
hibridnim algoritmima koriste algoritmi lokalne pretrage (eng. Local Search, LS). Za rješavanje
problema krojenja korišten je hibridni algoritam o kojem je pisao Falkenauer
[9], koji za lokalnu pretragu koristi modificirani kriterij dominiranja (eng. Dominance Criterion).
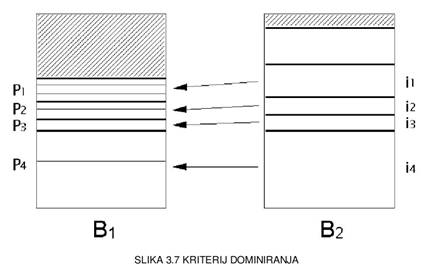
Kriterij dominiranja je definiran
kao: "ako uzmemo 2 spremnika B1 i B2, te ako postoji podskup {i1, ... in}
predmeta iz B2 i raspodjela {P1, ... Pn} predmeta iz B1 takav da za svaki ii ne
postoji veći odgovarajući Pi, može se reći da B2 dominira nad B1
zato što rješenje koje sadrži B2 ne zahtjeva više spremnika od rješenja koje
sadrži B1" [9] (Slika 3.7.). Ovdje je kriterij izražen u sklopu problema
smještanja predmeta (eng. Bin packing
Problem, BPP), no kao što je već rečeno, problem smještanja
predmeta i problem krojenja spadaju u srodnu grupu problema, te često
predstavljaju isti problem optimizacije [1].
Za korištenje u
sklopu grupirajućeg genetskog algoritma, kriterij dominiranja je
promijenjen i obavlja funkciju lokalne optimizacije na sljedeći
način: prilikom reprodukcije u grupirajućem genetskom algoritmu, bilo
da se reprodukcija izvodi križanjem ili mutacijom, prije nego se
neraspoređeni predmeti smjeste u nove grupe, provodi se provjera da li
neki od tih predmeta može zamijeniti bilo koja dva predmeta iz iste grupe, a da
se ne premaši duljina materijala od kojeg se grupa reže. Ukoliko se nađu
zamjene koje se mogu ostvariti, provede ih se. Rezultat ovakve zamjene su dvije
bitne stvari:
·
prvi
(i očiti) rezultat je bolje iskorištavanje materijala koji se reže (manje
ostataka nakon rezanja)
·
drugi
rezultat je oslobađanje manjih predmeta za smještanje u grupe, što
omogućuje bolje pakiranje neraspoređenih materijala (kao i nastavak
lokalnog pretraživanja tj. zamjena)
Ovaj postupak se
provodi dok god postoje zamjene koje je moguće ostvariti. Kad se više ne
nađe zamjena koju je moguće ostvariti, neraspoređeni predmeti se
slažu u grupe uobičajenim postupkom.
3.2.
Algoritmi za rješavanje 2D problema krojenja
Pošto je 2D
problem samo proširenje 1D problema, vrijede isti principi, što znači da i
za ovaj problem grupirajući genetski algoritam ima jednake prednosti kao i
za 1D problem. Ono što je posebno kod 2D problema rezanja je pojavljivanje
problema smještanja predmeta unutar materijala (zato se još to naziva i problem
2D smještanja). Naime, kod 1D problema krojenja nije bitan redoslijed
izrezivanja predmeta, osim ako je neprekidnost (eng. contiguity) jedno od ograničenja problema, dok je kod 2D
problema krojenja smještanje predmeta na materijal vrlo bitno [10]. Postoje 2
grane algoritama za smještanje predmeta: algoritmi koji koriste police i
algoritmi koji ne koriste police [11]. Algoritmi koji koriste police se
najčešće koriste za smještanje predmeta u role (materijal fiksne
širine i neodređene visine), a za rješavanje problema smještanja u
spremnike (materijal fiksne širine i visine) se koriste algoritmi koji ne koriste
police.
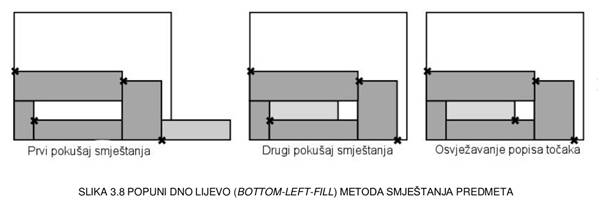
Jedan od
poznatijih algoritama koji ne koriste police je popuni dno lijevo algoritam
(eng Bottom-Left-Fill, BLF) [10].
Ovaj algoritam sadrži popis točaka u koje se može smjestiti donji lijevi
kut predmeta. Krenuvši od najniže najljevije točke, ispituje se da li se
predmet može smjestiti u danu točku bez da izlazi izvan granica materijala
i da se ne preklapa sa drugim predmetima. I tako se ide redom po listi svih
mogućih točaka smještanja. Ako se nađe točka u koju se predmet
može smjestiti, predmet se smjesti a lista točaka se osvježi tako da se
obriše iskorištena točka a dodaju gornji lijevi i doljnji desni kut
predmeta smještenog na materijal (Slika 3.8.). Ako se predmet ne može smjestiti
ni u jednu točku iz liste, onda predmet ne stane u materijal tj. ne može
se od njega izrezati. Ovakvim postupkom, za razliku od ostalih algoritama za
smještanje, ovaj algoritam može popuniti "rupe" nastale smještanjem
ranijih predmeta na materijal.
Grupirajući genetski algoritam
spomenut kod rješavanja 1D problema krojenja je, uz promjenu zapisa rješenja te
izvedbe generiranja grupa, križanja i mutacije, prikladan i za rješavanje 2D
problema rezanja.
Grupe, osim
popisa predmeta koji se režu i dimenzija materijala iz kojega se režu, još
sadrže i popis točaka u koje pojedini predmet smještamo. Generiranje grupa
se izvodi slično kao i kod 1D problema: nasumično se odabere jedan od
neiskorištenih predmeta, slučajnim odabirom se provjeri da li se predmet
rotira ili ne, te ga se pokuša smjestiti u grupu koristeći BLF algoritam.
Ako predmet ne stane u grupu, rotira ga se i ponovo pokuša smjestiti u grupu
(znači ispituje se da li predmet stane u grupu normalno ili rotirano). Ako
i nakon rotacije predmet ne stane u grupu, briše ga se sa liste predmeta koje
se pokušava smjestiti u grupu. Kad se lista predmeta koje pokušavamo smjestiti
isprazni, znači ili više nema slobodnih predmeta ili više ne stane ni
jedan u grupu, grupa je gotova. Ponavljanjem ovog postupka se generiraju
jedinke. A taj postupak se koristi i prilikom križanja i mutacije za grupiranje
neiskorištenih predmeta. Za evaluaciju se koristi ista funkcija kao i za 1D
problem krojenja, samo se umjesto preostale duljine materijala koristi
preostala površina materijala.
Od algoritama za
smještanje koji koriste police spomenut ćemo hibridni prvi
odgovarajući algoritam (eng. Hybrid-First-Fit,
HFF) [11]. Kao što i naziv grupe algoritama govori, ovaj algoritam ne smješta
predmete slobodno na materijal, nego ih slaže u razine. Prvi predmet koji se
slaže se stavlja u lijevi kut na bazu materijala. Taj predmet određuje
visinu početne razine, tako da u istu razinu (policu) mogu doći samo
predmeti koji su jednako visoki ili niži od tog predmeta. Za svaki idući
predmet se redom provjerava da li stane u neku od postojećih razina, te
ako stane da se smjesti u prvu razinu u koju može stati. Ako predmet ne stane u
nijednu razinu, za njega se otvori nova razina. Ovaj korak je identičan
izvođenju algoritma prvi odgovarajući (eng. First-Fit, FF) kojeg se može vidjeti na slici 3.9.
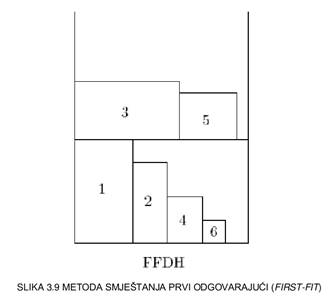
Ovakav način smještanja
predmeta je vrlo povoljan za problem pakiranja u role, za probleme sa
giljotinskim rezovima te za probleme gdje je brzina dolaska do rješenja
ključna (na račun kvalitete rješenja).
Da bi se ovaj
algoritam mogao koristiti za smještanje predmeta na materijale sa definiranom
visinom, potrebno je razine stvorene gore opisanim načinom sortirati da
stanu na materijale (što se svodi na 1D problem krojenja [11]). Zbog toga se
hibridni prvi odgovarajući algoritam naziva dvofazni algoritam sa policama.
Prilikom
korištenja ove metode smještanja sa grupirajućim genetskim algoritmom, ne
može se provoditi dvofazno rješavanje. Zbog toga je algoritam promijenjen na
sljedeći način: ako predmet ne stane u trenutne razine, smješta ga se
u novu razinu samo ako se time neće premašiti visina materijala, a u
suprotnom ga se smješta na drugi materijal. Time je omogućeno da se ne
mora mijenjati način na koji se generiraju grupe koje tvore rješenje.
4. Praktični dio
4.1.
Programski sustav
4.1.1. Opis
programskog sustava
Programski dio
završnog zadatka rađen je u programskom jeziku Java. Za rješavanje 1D
problema krojenja implementirani su grupirajući genetski algoritam (GGA)
te hibridni grupirajući genetski algoritam (HGGA). Grupirajući
genetski algoritam je implementiran u generacijskom i eliminacijskom modelu
modelu (SSGGA). Također, isti algoritam implementiran je sa
deterministički promjenjivim (AGGA, ASSGGA) te sa samo-adaptivno (SAGGA)
promjenjivim parametrima [8]. Deterministički algoritam mijenja
vjerojatnost križanja, mutacije i veličinu populacije, a samo-adaptivni
mijenja samo vjerojatnosti križanja i mutacije. Za rješavanje 2D problema
krojenja implementirani su grupirajući genetski algoritmi koji za
smještanje predmeta koriste popuni dno lijevo metodu smještanja (BLF) odnosno
hibridni prvi odgovarajući metodu smještanja (HFF).
4.1.2.
Optimizacijski problemi
Od 1D problema
krojenja za rješavanje odabran je 1/V/D/M problem. Prema [1], kako je ranije
opisano, to je jednodimenzionalni problem odabira materijala da bi se
izrezali svi predmeti, gdje postoji više
materijala različitih duljina, a predmeta je puno i to u puno
različitih duljina. Lako je vidjeti da algoritmi koji rješavaju ovaj
problem lako mogu riješiti bilo koji 1/V/I/ i 1/V/D/ problem. Kao dodatni
parametri problema se zadaju debljina rezne ploče (gubitak pri rezanju) i
maksimalni dopušteni ostatak da bi se materijal smatrao dobro iskorištenim.
Od 2D problema
krojenja za rješavanje odabran je 2/V/I/M problem, sa dodatnim
ograničenjem RF. Prema [1] i [3], kako je ranije opisano, to je
dvodimenzionalni problem odabira materijala da bi se izrezali svi predmeti,
gdje: postoji više materijala istih dimenzija, predmeta je puno i to u puno
različitih dimenzija, dopušteno je rotirati predmete za 90° te su dopušteni
slobodni rezovi.
4.1.3.
Programsko okruženje
Algoritmi za
rješavanje 1D problema rezanja su prilagođeni za korištenje unutar
programskog okruženja ostvarenog u sklopu predmeta Projekt (Slika 4.1.), no
postoji prilagođena verzija za samostalno pokretanje. U slučaju
samostalnog pokretanja, algoritmi kao argument primaju naziv ulazne i izlazne
datoteke (tim redosljedom). U obje datoteke duljine su izražene u milimetrima.
Ulazna datoteka mora imati u prvom redu odvojeno tabulatorom (znak '\t') maksimalno
vrijeme izvođenja (u milisekundama), debljinu reza te maksimalni dopušteni
gubitak. U idućim redovima treba biti duljina materijala i količina
materijala (-1 označava beskonačnu količinu) odvojeni
tabulatorom. Nakon takvog popisa svih materijala, treba biti red crtica (znak
'-') a zatim popis predmeta jednakog formata kao popis materijala. U izlaznu
datoteku se zapisuje ukupna iskorištenost te ukupno vrijeme izvođenja.
Osim ulazne i izlazne datoteke, algoritmi koriste još i datoteku sa parametrima.
Ta datoteka je istog imena kao i algoritam, sa nastavkom '_param.txt', a u njoj
se nalaze (početni) parametri algoritama. U izlaznoj datoteci se u svakom
redu nalazi duljina materijala koji se reže te tabulatorom odvojen popis
predmeta koji se od tog materijala režu. Nakon popisa materijala se nalazi
postotak iskorištenosti materijala.
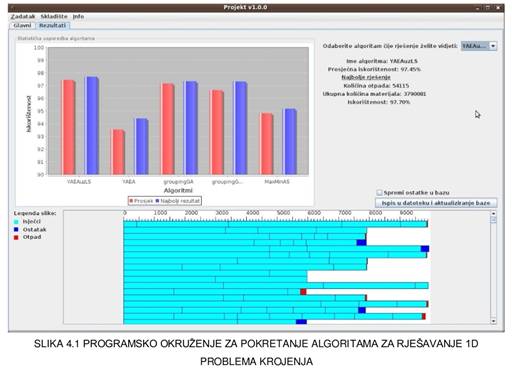
Za 2D problem rezanja algoritmi kao
argument primaju naziv ulazne datoteke, naziv izlazne datoteke te naziv
datoteke sa slikama rješenja. Ulazna datoteka je neznatno izmjenjena: u prvom
redu se nalaze redom širina materijala, visina materijala te maksimalni ostatak
(površina), razdvojeni tabulatorom. U ostalim redovima se nalaze sirina
predmeta, visina predmeta i količina predmeta, također odvojeni
tabulatorom. U izlaznoj datoteci se za svaki materijal nalazi popis predmeta
zabilježen doljnjim lijevim i gornjim desnim kutom predmeta koji se od tog
materijala izrezuje. Datoteka sa slikama rješenja je u PDF formatu (naziv
izlazne datoteke koji se predaje mora imati .pdf ekstenziju) te se na svakoj
stranici nalazi po jedna slika koja predstavlja položaj predmeta u jednom
materijalu.
4.2.
Eksperimenti
4.2.1. 1D
problem krojenja
Nakon što je
implementacija algoritama privedena kraju, potrebno je podesiti parametre
algoritama (onih koji neće mijenjati iznose parametara tijekom
izvođenja). Pošto smo već naveli da se takva podešavanja rade
eksperimentalno, oba modela grupirajućeg genetskog algoritma (generacijski
i eliminacijski) su pokrenuta po 10 puta za isti problem za sve kombinacije sljedećih
parametara:
• veličina populacije [30, 50,
70, 100]
• vjerojatnost križanja [0.5, 0.55,
0.6, 0.65, 0.7, 0.75, 0.8, 0.85, 0.9]
• vjerojatnost mutacije [0.05, 0.1,
0.15, 0.2, 0.25, 0.3, 0.35, 0.4, 0.45, 0.5]
Ostali parametri
(elitizam i broj generacija/reprodukcija) su bili fiksni.
Problem
pomoću kojeg su se provodili eksperimenti za podešavanje parametara je
sadržavao materijale: duljine 10000, 6000 i 5000 beskonačno komada
(materijal koji se može nabaviti ili sl.), duljine 640 i 3548 po 3 komada, duljine
1640, 614 i 496 po 2 komada i duljine 574 i 625 po 1 komad. Predmeti koje je
trebalo rezati su bili: 20 komada duljine 6432, 150 komada duljine 1640, 80
komada duljine 654, 150 komada duljine 2987, 80 komada duljine 852, 80 komada
duljine 4741, 60 komada duljine 3256, 50 komada duljine 4256, 80 komada duljine
3321, 130 komada duljine 3700, 130 komada duljine 1910, 150 komada duljine
1236, 100 komada duljine 2356, 130 komada duljine 1055, 80 komada duljine 963,
100 komada duljine 2876 i 130 komada duljine 420. Debljina rezne ploče je
5 a maksimalni dopušteni ostatak 200.
Rezultati
ispitivanja su očekivano pokazali da generacijski algoritam postiže bolje
rezultate za veću populaciju (veće područje pretrage i više
novih jedinki stvoreno). Za eliminacijski algoritam razlike prosjeka za
populaciju od 100 i populaciju od 70 gotovo da i nema, ali se razlika
povećava što se više smanjuje broj jedinki. To je u skladu sa
očekivanjima, jer unatoč tome što veća populacija osigurava
veće područje pretrage rješenja, isto tako smanjuje šansu svake
pojedine jedinke da bude izabrana za reprodukciju. Slike 4.2. - 4.5. prikazuju
odnos promjena parametara vjerojatnosti mutacije i križanja i prosjeka
iskorištenosti za oba algoritma.
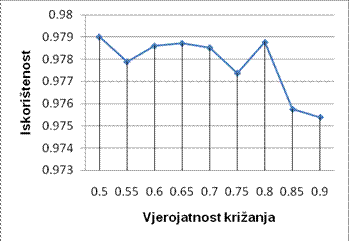
Slika 4.2 generacijski grupirajući genetski algoritam
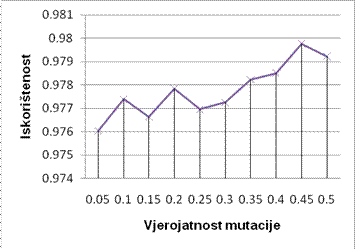
Slika 4.3 GENERACIJSKI GRUPIRAJUĆI GENETSKI ALGORITAM
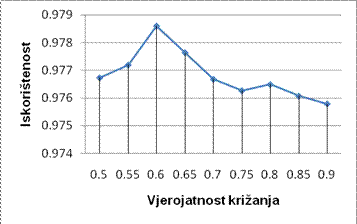
Slika 4.4 eliminacijski GRUPIRAJUĆI GENETSKI ALGORITAM
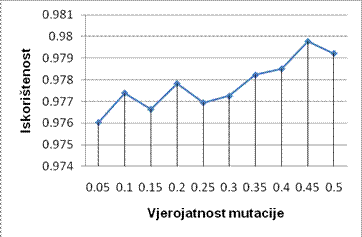
Slika 4.5 eliminacijski GRUPIRAJUĆI GENETSKI ALGORITAM
Iz tablica se
lako može očitati da su za generacijski algoritam optimalni parametri:
• veličina populacije = 100
• vjerojatnost križanja = 0.5 (50%)
• vjerojatnost mutacije = 0.45 (45%)
Dok su za
eliminacijski algoritam optimalni parametri:
• veličina populacije = 100 ili
70 (ovisno o vremenskim zahtjevima)
• vjerojatnost križanja = 0.6 (60%)
• vjerojatnost mutacije = 0.45 (45%)
Primijetimo i to
da su ukupne razlike u parametrima između algoritama minimalne bez obzira
na njihov drastično drugačiji način rada.
Sa ovako
podešenim parametrima provedeno je međusobno ispitivanje svih
implementiranih verzija grupirajućeg genetskog algoritma. Problem za
ispitivanje algoritama je sadržavao materijale: duljine 10000 i 6000
beskonačno komada (materijal koji se može nabaviti ili sl.), duljine 2300
80 komada, duljine 1200 50 komada, duljine 4500 70 komada i duljine 8000 40
komada. Predmeti koje je trebalo rezati su bili: 30 komada duljine 530, 30
komada duljine 780, 30 komada duljine 1080, 30 komada duljine 1360, 30 komada
duljine 1700, 30 komada duljine 1950, 30 komada duljine 2330, 30 komada duljine
2800, 60 komada duljine 3400, 60 komada duljine 4130, 60 komada duljine 4750,
60 komada duljine 5200, 60 komada duljine 5870, 60 komada duljine 6300, 30
komada duljine 6950, 30 komada duljine 7470 i 30 komada duljine 8100. Debljina
rezne ploče postavljena je na 3 a maksimalni dopušteni ostatak na 200.
Svaki algoritam se pokretao 40 puta. Rezultati ispitivanja iskorištenosti
materijala se mogu vidjeti u tablici 1.
Tablica 4.1 rezultati ispitivanja
|
Algoritam |
HGGA |
GGA |
SSGGA |
AGGA |
ASSGGA |
SAGGA |
|
Maksimum |
96.08% |
96.28% |
96.27% |
96.08% |
95.95% |
95.07% |
|
Prosjek |
94.79% |
94.73% |
94.25% |
94.77% |
94.37% |
93.47% |
4.2.2. 2D
problem krojenja
Zbog korištenja
gotovo nepromijenjenog grupirajućeg genetskog algoritma s kakvim je
rješavan 1D problem krojenja, dodatna optimizacija parametara se nije
provodila, nego su samo kopirane vjerojatnosti križanja i mutacije. Sa jednakim
genetskim algoritmom koristimo 2 algoritma za smještanje predmeta na materijal,
pa zbog toga rezultati više govore o algoritmima za smještanje predmeta nego o
samim genetskim algoritmima.

Problem za ispitivanje algoritama je
sadržavao materijal širine 100 i visine 70. Predmeti koje je trebalo rezati su
bili: 10x10 90 komada, 30x15 60 komada, 15x35 120 komada, 20x25 75 komada,
20x10 100 komada, 15x20 150 komada, 25x15 40 komada i 30x10 60 komada.
Maksimalni ostatak je postavljen na 200. Oba algoritma su pokrenuta po 10 puta
(nisu uočene velike razlike u nađenim rezultatima u različitim
pokretanjima da bi bilo opravdano provesti više pokretanja). Zapis rezultata 2D
krojenja slikom je prikazan na slici 4.6.
4.3. Zaključna razmatranja
Kod ispitivanja
djelotvornosti algoritama za rješavanje 1D problema krojenja, rezultati su vrlo
slični, ali se ipak iz njih mogu izvući neki zaključci. Treba
imati na umu, da najbolje pronađeno rješenje nema veliku ulogu u
ocjenjivanju rada pojedinog algoritma zbog njihove nedeterminističke
prirode (kvaliteta rješenja podložna "sreći" u pretraživanju prostora
rješenja). Zato se iz prosjeka pronađenih rješenja mogu bolje vidjeti
razlike među algoritmima.
Algoritam koji je
ostvario najlošiji rezultat je samo-adaptivni genetski algoritam. Razlog tako
lošem rezultatu je što algoritam ima veliku šansu (s obzirom na broj generacija
i veličinu populacije) producirati jedinku koja će u danom trenutku
biti dosta bolja od ostalih iz populacije (a time i imati veću šansu za
odabir za reprodukciju) a imati u sebi zapisane parametre koji ne podupiru
daljnje širenje po prostoru mogućih rješenja. Time se efektivno prekida
traženje boljeg rješenja te algoritam zaglavljuje u lokalnom optimumu.
Generacijski
algoritmi su nešto uspješniji od svojih eliminacijskih inačica zbog
veće prednosti koje daju boljim rješenjima, dok kod eliminacijskog
algoritama sve jedinke imaju jednaku šansu za reprodukciju. S druge strane,
eliminacijski algoritmi su jednostavniji za implementaciju te brže obavljaju
selekciju.
Adaptivni
algoritmi su također uspješniji od svojih "običnih"
inačica. Treba se još uzeti u obzir da se za podešavanje parametara
"običnih" inačica potrošilo po 8 sati na optimizaciju
parametara, za razliku od adaptivnih gdje je naći formulu po kojoj će
se mijenjati parametri bilo vrlo brzo i jednostavno.
Hibridni genetski
algoritam potpomognut lokalnom pretragom je očekivano ostvario najbolji
rezultat, te bi na nekom zahtjevnijem problemu sigurno povećao razliku
između sebe i ostalih genetskih algoritama.
Kod algoritama za
rješavanje 2D problema krojenja, genetski algoritam koji je koristio popuni dno
lijevo (BLF) metodu smještanja predmeta je očekivano postigao puno bolje
rezultate od algoritma koji je koristio modificiranu hibridni prvi
odgovarajući (HFF) metodu smještaja predmeta (95.7% iskorištenosti naspram
88.9%). S druge strane, algoritam sa hibridnom prvi odgovarajući metodom
smještaja se izvodio neusporedivo brže: prosjek od 12.77 sekundi za 1000
generacija nasuprot prosjeka od 11.68 sekundi za 100 generacija algoritma koji
je koristio popuni dno lijevo metodu. Osim što takva brzina izvođenja može
biti presudna kod izuzetno velikih problema, metoda smještanja hibridni prvi
odgovarajući generira rezultate koji se mogu rezati giljotinskim rezovima
što isto može biti jedan od zahtjeva.
5.
Zaključak
Genetski
algoritmi su vrlo moćan alat za rješavanje optimizacijskih problema, za
koje ne postoje deterministički algoritmi koji mogu za veće probleme
pronaći optimalno rješenje u nekom razumnom vremenu. Problem krojenja je
jedan od takvih problema. Za rješavanje problema krojenja posebno je pogodan
grupirajući genetski algoritam, koji je svojim zapisom rješenja posebno
prilagođen prirodi problema krojenja i smještanja.
Iz rezultata
ispitivanja i vremena utrošenog na eksperimentalno podešavanje parametara jasno
je vidljivo da je adaptivna kontrola parametara potpuno superiorna
statičkom postavljanju parametara prije pokretanja algoritma. Čak i
pri odabiru lošije formule za podešavanje parametara, algoritam bolje
funkcionira nego ako se odaberu lošiji statički parametri.
Za dvodimenzionalni
problem krojenja se Bottom-Left-Fill metoda smještanja pokazala puno
učinkovitijom od Hybrid-First-Fit metode, dok se grupirajući
algoritam pokazao jednako prikladan za rješavanje 2D kao i 1D problema
krojenja.
6.
Literatura
[1] H. Dyckhoff, A typology of cutting and packing
problems, European Journal of Operational Research, vol. 44, pp. 145-159, 1990.
[2] Constantine Goulimis, s
Interneta, Wikipedia, Cutting stock
problem, http://en.wikipedia.org/wiki/Cutting_stock_problem, Svibanj 2008.
[3] Lodi A., Martello S., Vigo D., Heuristic and
Metaheuristic Approaches for a Class of Two-Dimesional Bin Packing Problems,
INFORMS Journal on Computing. Volume 11, 4. izdanje (Travanj 1999) 345 – 357.
[4] Wu, A. S., Lindsay, R. K., & Riolo, R. L.
(1997), Empirical observations on the roles of crossover and mutation,
Proceedings of the Seventh International Conference on Genetic Algorithms,
362–369.
[5] E. Falkenauer, Applying genetic algorithms to
real-world problems, L. D. Davis, K. De Jong, M. D. Vose i L. D. Whitley,
urednici, Evolutionary Algorithms, str. 65-88, Springer, New York, 1999
[6] R. Hinterding, L. Khan, Genetic algorithms for
cutting stock problems: with and without contiguity, Progress in Evolutionary
Computation (X. Yao, urednik), vol. 956, Lecture Notes in Artificial
Intelligence, Berlin, pp. 166-186, Springer, 1995
[7] E. Falkenauer , A. Delchambre, A Genetic
Algorithm for Bin Packing and Line Balancing, in "Proc. of the IEEE 1992
Int. Conference on Robotics and Automation (RA92)", Svibanj 10-15, 1992,
Nice, France.
[8] A. E. Eiben, R. Hinterding, Z. Michalewicz,
Parameter Control in Evolutionary Algorithms, IEEE Transactions on Evolutionary
Computation, vol. 3, no. 2, pp. 124-141, 1999
[9] E. Falkenauer, A hybrid grouping genetic
algorithm for bin packing, Journal of Heuristics, 2:5 30, 1996
[10] Hopper E., Turton B.C.H., A Genetic Algorithm
for a 2D Industrial Packing Problem, Computers and Industrial Engineering, vol.
37/1-2 (1999), 375-378.
[11] Lodi A., Martello S., Monaci M., Two
dimensional packing problems: A survey, European Journal of Operational
Research, 141 (2002), 241–252
Uporaba genetskih algoritama za rješavanje
problema krojenja
Sažetak: Problem krojenja pripada grupi problema kod kojih je cilj na neki
način grupirati elemente skupa u manje podskupe. Za rješavanje te grupe
problema se vrlo dobrim pokazao grupirajući genetski algoritam. U ovom
radu uspoređeni su rezultati rješavanja problema ''običnim''
grupirajućim genetskim algoritmom, njegovom verzijom sa promjenjivim
parametrima te hibridnim genetskim algoritmom.
Ključne riječi: Problem krojenja, grupirajući genetski
algoritam, hibridni genetski algoritam, kontrola parametara
Using Genetic
Algorithm for solving cutting stock problem
Abstract: Cutting stock problem belongs to a group of problems where the goal is to
group together members of a set into subsets. Grouping Genetic Algorithm has
shown to be very convenient for solving that kind of problems. In this paper
results from ''ordinary'' Grouping Genetic Algorithm, Hybrid Grouping Genetic
Algorithm and (Deterministic) Adaptive Grouping Genetic Algorithm are compared.
Keywords: Cutting stock problem, Grouping Genetic Algorithm, Hybrid Genetic Algorithm, parameter control